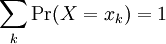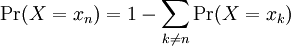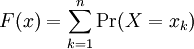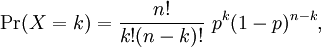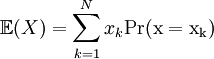機率

 

Random variable 

1. A discrete random variable X is a quantity that can assume any value x from a discrete list of values with a certain probability.
2. The probability that the random variable X assumes the particular value x is denoted by Pr(X = x). This collection of probabilities, along with all possible values x, is the probability distribution of the random variable X.

Ex. Sum of two dices

X=4 ==> (1,3), (2,2) (3,1)

Discrete Probability Rules
Probabilities are numbers between 0 and 1: 0 ≤ Pr(X = xk) ≤ 1 for all k The sum of all probabilities for a given experiment (random variable) is equal to one:  The probability of an event is 1 minus the probability that any other event occurs:

Ex. Sum of two dices

Pr(X=3) = 2/36     ,   Pr(X=4) = 3/36     

Cumulative Distribution Function of a Discrete Random Variable
The cumulative distribution function (CDF) of a random variable X is denoted by F(x), and is defined as F(x) = Pr(X ≤ x). Using our identity for the probability of disjoint events, if X is a discrete random variable, we can write where xn is the largest possible value of X that is less than or equal to x

Binomial PDF
If X is a binomial random variable associated to n independent trials, each with a success probability p, then the probability density function of X is: where k is any integer from 0 to n. Recall that the factorial notation n! denotes the product of the first n positive integers: n! = 1·2·3···(n-1)·n, and that we observe the convention 0! = 1.

Definition: Expected Value of a Discrete Random Variable
The expected value, 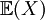, of a random variable X is weighted average of the possible values of X, weight by their corresponding probabilities: where N is the number of possible values of X.

References: 

[1] https://blogs.ubc.ca/math105/