機率

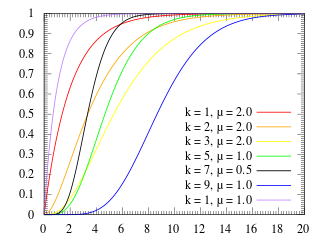
Erlang distribution

The Erlang distribution is a two parameter family of continuous probability distributions with support ${\displaystyle x\;\in \;[0,\,\infty )}$. The two parameters are:

• a positive integer 'shape' ${\displaystyle k}$ 
• a positive real 'rate' ${\displaystyle \lambda }$; sometimes the scale ${\displaystyle \mu }$, the inverse of the rate is used.

The Erlang distribution with shape parameter ${\displaystyle k}$ equal to 1 simplifies to the exponential distribution. It is a special case of the Gamma distribution. It is the distribution of a sum of ${\displaystyle k}$ independent exponential variables with mean 1/ λ each.

The Erlang distribution was developed by A. K. Erlang to examine the number of telephone calls which might be made at the same time to the operators of the switching stations. T

Events that occur independently with some average rate are modeled with a Poisson process.

The waiting times between k occurrences of the event are Erlang distributed. 

The Erlang distribution, which measures the time between incoming calls, can be used in conjunction with the expected duration of incoming calls to produce information about the traffic load measured in erlangs.

The number of events in a given amount of time is described by the Poisson distribution.

Poisson distribution

統計與機率學裡常見到的離散機率分佈，由法國數學家西莫恩·德尼·帕松（Siméon-Denis Poisson）在1838年時發表。

Poisson分佈適合於描述單位時間內隨機事件發生的次數的機率分佈。如某一服務設施在一定時間內受到的服務請求的次數，電話交換機接到呼叫的次數、汽車站台的候客人數、機器出現的故障數、自然災害發生的次數、DNA序列的變異數、放射性原子核的衰變數、雷射的光子數分佈等等。

An event can occur 0, 1, 2, … times in an interval. The average number of events in an interval is designated ${\displaystyle \lambda }$ (lambda). Lambda is the event rate, also called the rate parameter. The probability of observing k events in an interval is given by the equation

probability mass function (PMF) for a Poisson distribution.

${\displaystyle P(k{\text{ events in interval}})={\frac {\lambda ^{k}e^{-\lambda }}{k!}}}$

where

• ${\displaystyle \lambda }$ is the average number of events per interval
• e is the number 2.71828... (Euler's number) the base of the natural logarithms
• k takes values 0, 1, 2, ….

Poisson分佈的參數λ是單位時間（或單位面積）內隨機事件的平均發生次數。
期望值 決定常態分配的曲線外觀

=1, 0*0.37+1*0.37+2*0.19+3*0.07+5*0.000+6*0.0000=~1
=10, 平均值在中間 (0~20) 為一個常態分配

Examples of probability for Poisson distributions[edit]

On a particular river, overflow floods occur once every 100 years on average. Calculate the probability of k = 0, 1, 2, 3, 4, 5, or 6 overflow floods in a 100-year interval, assuming the Poisson model is appropriate.

Because the average event rate is one overflow flood per 100 years, λ = 1

${\displaystyle P(k{\text{ overflow floods in 100 years}})={\frac {\lambda ^{k}e^{-\lambda }}{k!}}={\frac {1^{k}e^{-1}}{k!}}}$

${\displaystyle P(k=0{\text{ overflow floods in 100 years}})={\frac {1^{0}e^{-1}}{0!}}={\frac {e^{-1}}{1}}=0.368}$

${\displaystyle P(k=1{\text{ overflow flood in 100 years}})={\frac {1^{1}e^{-1}}{1!}}={\frac {e^{-1}}{1}}=0.368}$

${\displaystyle P(k=2{\text{ overflow floods in 100 years}})={\frac {1^{2}e^{-1}}{2!}}={\frac {e^{-1}}{2}}=0.184}$

參考:

1. Poisson分布~曹亮吉 http://episte.math.ntu.edu.tw/articles/sm/sm_16_07_1/
2. https://en.wikipedia.org/wiki/Poisson_distribution

Pareto distribution

Consider a population of households and suppose sampling household incomes is like sampling from a Pareto[10000,2]. What proportion of people earn more than $100000? From the form of the survival function, it should be obvious that the answer is 1%: only 1 in 100 households earn more than $100000. 

f X is a random variable with a Pareto (Type I) distribution,^[1] then the probability that X is greater than some number x, i.e. the survival function (also called tail function), is given by

${\displaystyle {\overline {F}}(x)=\Pr(X>x)={\begin{cases}\left({\frac {x_{\mathrm {m} }}{x}}\right)^{\alpha }&x\geq x_{\mathrm {m} },\\1&x<x_{\mathrm {m} },\end{cases}}}$

Exponential distribution

1. In probability theory and statistics, the exponential distribution (a.k.a. negative exponential distribution) is the probability distribution that describes the time between events in a Poisson process, i.e. a process in which events occur continuously and independently at a constant average rate. 
2. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson processes, it is found in various other contexts.

短距離無線通訊比較: Wi-Fi, BT, Zigbee, Thread

Pi GPIO 輸出電流其實有30mA.

今天做了一個實驗: 量測Pi GPIO的輸出電流, 經查資料都說是 16mA, 今天量測GPIO輸出,
用三用電錶梯電流檔量測, 輸出電流是30m~40mA (在只有一根輸出的情況下)

使用Wireshark 用過濾Wi-Fi 802.11的封包

使用Wireshark 用過濾Wi-Fi 802.11的封包

filter 語法: 

# 過濾 MAC 來源位址
wlan.sa == xx:xx:xx:xx:xx:xx 

# 過濾 MAC 目的位址

wlan.da == xx:xx:xx:xx:xx:xx

# 過濾 MAC 位址 (不管出現在來源或目的位址) 

wlan.addr == xx:xx:xx:xx:xx:xx

馬可夫鏈 (Markov Chain)

1) Random Variable X

2) Random Process (Stochastic Process) {X(t), t>=0} , 是一個Random Variable 的集合, (t可以是discrete time or continuous time)

3) Markov Process, 也是 Random Process,此Random Process {Xi,i=0,1,2....}是在描述狀態轉移的過程 (所有你會有一群狀態序列Chain), 但此系統的行為是chain中的節點，只和相鄰的節點有關，即你下一個狀態是什麼只取決你上一個狀態有關,而和先前的狀態無關 (此行為是是Markov property, 即Memory-less)

a discrete-time  Markov Process-->  Markov chain(DTMC)

a continuous-time Markov process--> Markov chain (CTMC)

4) Renewal process : is a counting process in which the inter-arrival times are an iid random sequence

  

     在講時間，事件發生的間隔時間為一個隨機變數Ti , 若Ti 彼'此為iid 則此counting process為renewal process。 (只看時間，不看狀態)

 
5) Markov Renewal Process

將 Markov process 再加上時間, 則狀態轉換和時間產生了關係。 Markov Renewal Process 共包含了2個隨機變數 {Xi,Ti}，狀態是一個隨機變數，時間也是一個隨機變數。也許我們想關心，在這個狀態待多久後會跳到下一個狀態。

Consider a state space  Consider a set of random variables , where  are the jump times and  are the associated states in the Markov chain (see Figure). Let the inter-arrival time, . Then the sequence  is called a Markov renewal process if

6) Semi-Markov process 

1. If we define a new stochastic process  for , then the process  is called a semi-Markov process. Note the main difference between an MRP and a semi-Markov process is that the former is defined as a two-tuple of states and times, whereas the latter is the actual random process that evolves over time and any realisation of the process has a defined state for any given time. The entire process is not Markovian, i.e., memoryless, as happens in a continuous time Markov chain/process (CTMC). Instead the process is Markovian only at the specified jump instants. This is the rationale behind the name, Semi-Markov.^[1][2][3] (See also: hidden semi-Markov model.)

Semi-Markov process 和Markov process的差異是,

會進入到某一個狀態 Xn ,只會發生在特定的時間區間,而不是發生在所有的時間點，因此，Semi-Markov Process 其Markovian 特性 (即memory-less的特性), 只會在特定時間而已 ，而非任意時間區間) 。即在Xn狀態只有和上一個狀態有關。而會落在上一個狀態其時間點也是特定的。

(defined in the above bullet point) where all the holding times are exponentially distributed is called a CTMC. 

Ergodic

A random process is ergodic if its time average is the same as its average over the probability space, 

在某一段時間的平均, X/Ti 和 整個時間的平均 X /T 是相同, 則稱為ergodic

Markov Model  ( 所有狀能已知)

馬可夫模型是一連串事件(狀態)接續發生的機率
馬可夫鏈（英語：Markov chain），又稱離散時間馬可夫鏈（discrete-time Markov chain，縮寫為DTMC^[1]），因俄國數學家安德烈·馬可夫（俄語：Андрей Андреевич Марков）得名，為狀態空間中經過從一個狀態到另一個狀態的轉換的隨機過程。

A Markov chain is a stochastic process with the Markov property. The term "Markov chain" refers to the sequence of random variables such a process moves through, with the Markov property"memorylessness"). defining serial dependence only between adjacent periods (as in a "chain").

It can thus be used for describing systems that follow a chain of linked events, where what happens next depends only on the current state of the system.

 已定義所有的狀態, 並有定義好從狀態 i 到各個狀態 j 的機率, 若共有N個狀態, 這就有一個矩陣描述每一個狀態彼此間的轉移的機率, ,這就狀態轉移機率矩陣 (State Transition probability matrix)

存在在一個狀態序列

常問的問題:

1. 我們也許想知道, 原本在S0 狀態，經過T步後, 會落在那一個狀態? ( 這會需要知道 Pij : 狀態i 到 j 的機率)
2. S0-->S1-->S2, 一開始在S0走2步後, 出現在S2的機率為何? 

Relation to other stochastic processes[edit]

1. 
   

1. A semi-Markov process (defined in the above bullet point) where all the holding times are exponentially distributed is called a CTMC. In other words, if the inter-arrival times are exponentially distributed and if the waiting time in a state and the next state reached are independent, we have a CTMC.

   ${\displaystyle \Pr(\tau _{n+1}\leq t,X_{n+1}=j|(X_{0},T_{0}),(X_{1},T_{1}),\ldots ,(X_{n}=i,T_{n}))=\Pr(\tau _{n+1}\leq t,X_{n+1}=j|X_{n}=i)}$

   ${\displaystyle =\Pr(X_{n+1}=j|X_{n}=i)(1-e^{-\lambda _{i}t}),{\text{ for all }}n\geq 1,t\geq 0,i,j\in \mathrm {S} }$

2. The sequence ${\displaystyle X_{n}}$ in the MRP is a discrete-time Markov chain. In other words, if the time variables are ignored in the MRP equation, we end up with a DTMC.

   ${\displaystyle \Pr(X_{n+1}=j|X_{0},X_{1},\ldots ,X_{n}=i)=\Pr(X_{n+1}=j|X_{n}=i)\,\forall n\geq 1,i,j\in \mathrm {S} }$

3. If the sequence of ${\displaystyle \tau }$s are independent and identically distributed, and if their distribution does not depend on the state ${\displaystyle X_{n}}$, then the process is a renewal process. So, if the states are ignored and we have a chain of iid times, then we have a renewal process.

   ${\displaystyle \Pr(\tau _{n+1}\leq t|T_{0},T_{1},\ldots ,T_{n})=\Pr(\tau _{n+1}\leq t)\,\forall n\geq 1,\forall t\geq 0}$

    事件發生的時間和狀態都無關(不論狀態是過去,現在或未來的狀態)

Hidden Markov Model  (存在未知狀態)


也許某些情況，我們無法或根本無法完整定義所有事件(狀態)的轉移機率矩陣 ,

圖來源: http://www.csie.ntnu.edu.tw/~u91029/HiddenMarkovModel.html#1

存在一個Hidden State ，不知道內部會怎麼選的機制, 而僅知道 S1,S2,S3狀態

在這個例子裡，有兩個事件的序列：一個是我觀察得到的；另一個是我看不到的，也就是對我來說是隱藏的，就是Hidden State。由於我知悉這兩個馬可夫鏈之間的關係，所以我便可以由其中一個馬可夫鏈的狀態，去預測另一個馬可夫鏈的狀態。而「隱馬可夫模型」，便是描述這樣的兩個序列的關係的統計模型。

HMM讓我們可以利用「看得到的」連 續現象去探究、預測另一個「看不到的」連續現象。

隱藏馬可夫模型的特色就是：我們只看到了觀察序列（果），但是我們看不到狀態序列（因）；我們只看到了依序噴出的 T 個值，但是我們看不到一路走過的是哪 T 個狀態。

References:

•  http://www.csie.ntnu.edu.tw/~u91029/HiddenMarkovModel.html#1
• https://en.wikipedia.org/wiki/Markov_renewal_process
• http://www.waelde.com/pdf/SchummDissertationCh4.pdf